
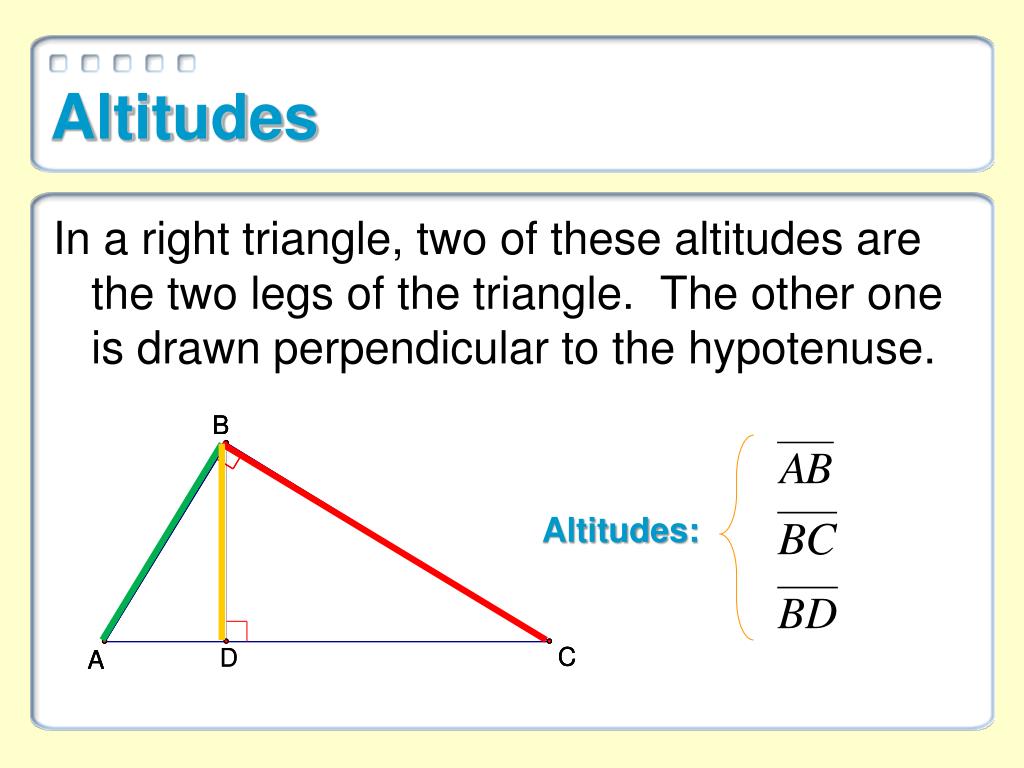
Length of a median can be calculated by the formula, In other words, the median divides the side into two halves. A Median is a line segment drawn from the centre of a side of the triangle to the opposite vertex. Know what is Altitude(geometry) and solved problems on Altitude(geometry).Altitude is used to calculate the area of a triangle, together with the length of the base to which the altitude is drawn.(5 points) Triangle DEF with altitude AE is shown. In other words, altitude represents the height of the triangle. proofs Question 1072035: Segment EA is an altitude of triangle DEF. The altitude of a triangle is the perpendicular line drawn from a vertex of the triangle to the opposite side.In an equilateral triangle, the median is the same as the altitude.Areas of the number of smaller portions that a median creates within a triangle would be always equal.If three medians are drawn at a time, they will surely meet at a point of the triangle.( Centroid ).The number of medians in a triangle would be always equal to the number of vertices in the triangle.The area of the two parts formed by drawing a median (which would be two triangles) would always be equal.An altitude begins from the vertex of a triangle and ends at the point of the opposite side which divides the opposite side equally. altitude definition 3: in geometry, a perpendicular line segment that extends from one vertex of a figure to the opposite edge or face, or the length of such a.There are some properties of a median that may be defined as its characteristics. In an equilateral triangle, the altitude is the same as the median.There can be up to three medians in a triangle, and when they all intersect, the intersection. Altitude is a basic component that helps to calculate the area of a triangle. For Triangles: a line segment leaving at right angles from a side and going to the opposite corner. An altitude can be a median of a triangle, as seen before with the equilateral and isosceles examples.Altitude is a part of a triangle that always needn’t be within the sides of a triangle.If all the altitudes of a triangle are drawn at a time, then the three altitudes will surely intersect at a point called the orthocentre.The angle that an altitude makes with the opposite side would always be 90 degrees. noun Mathematics The perpendicular distance from the base of a geometric figure to the opposite vertex, parallel side, or parallel surface.In other words, the number of sides in a triangle would be equal to the number of altitudes. Like the median, there would be 3 altitudes in a triangle.The properties can be different for different kinds of triangles, but there are some features or key properties that make them identifiable. The altitude and median of a triangle have different properties as a part of the triangle. Where, a, b and c are sides of the triangle and ‘a’ is the side to which the median is drawn. With the help of the length of sides, we can find the length of a median, using the below formula: Similarly, all the three medians divide the sides into equal halves. In the above figure, AR is a line segment that divides side BC into two halves, that is, BR and RC. The orthocenter of $\Delta ABC$ coincides with the circumcenter of $\Delta A'B'C'$ whose sides are parallel to those of $\Delta ABC$ and pass through the vertices of the latter.The median of a triangle is a line segment drawn from a vertex to another point on the opposite side of that vertex so that the line segment divides the opposite side into two halves. The foot of an altitude also has interesting properties. For example, due to the mirror property the orthic triangle solves Fagnano's Problem. I have collected several proofs of the concurrency of the altitudes, but of course the altitudes have plenty of other properties not mentioned below. Let's observe that, if $H$ is the orthocenter of $\Delta ABC$, then $A$ is the orthocenter of $\Delta BCH,$ while $B$ and $C$ are the orthocenters of triangles $ACH$ and $ABH,$ respectively. It is listed below, but appears on a separate page along with historical remarks. The earliest known proof was given by William Chapple (1718-1781). If a star has just set or is just about to rise, it is right at the horizon and has an altitude of 0 degrees. For example, if a star is directly overhead, its altitude is 90 degrees. It describes the angle between the horizon and some point in the sky.

The timing of the first proof is still an open question it is believed, though, that even the great Gauss saw it necessary to prove the fact. In astronomy, altitude has a somewhat different meaning. This is a matter of real wonderment that the fact of the concurrency of altitudes is not mentioned in either Euclid's Elements or subsequent writings of the Greek scholars.


 0 kommentar(er)
0 kommentar(er)
